2017洋泾中学高中三年级第一学期期中考
填空题
若复数
满足
（
为虚数单位），则复数=_________
已知,
，则
_________
过点
与直线
垂直的直线方程为________
关于
的不等式
的解集为
，则实数
的取值范围________
若
，则方程
的所有解之和等于_______
若对于任意实数，都有，则
的值为______
若数列
为等差数列，且，则
一圆柱的侧面展开图是边长为2的正方形，则此圆柱的体积为_______
设函数的概念域为，且为奇函数，当
时
，若在区间
上是单调递增函数，则
的取值范围______
10、双曲线
的一个焦点与抛物线
的焦点重合，且焦点到渐近线的距离为1，则此双曲线的实轴长为______
11、函数的概念域为实数集，满足
，在
时，
若在区间
上函数
恰有四个不一样的零点，则实数
的取值范围______
12、已知全集为
，概念集合
的特点函数为，对于
，给出下列四个结论:
（1）对任意
有
（2）对任意若
,则
（3）对任意
, 有
（4）对任意, 有
其中，正确的序号是_____
选择题
13、关于三个不同平面与直线，下列命题中的假命题是（ ）
A.若
，则内肯定没有直线平行于
B.若与不垂直，则内肯定没有直线垂直于
C.若
，则
D.若，则内所有直线垂直于
14、已知函数，数列的通项公式是
，那样“函数在上
单点递增”是“数列是递增数列”的（ ）
A.充分非必要条件 B.必要不充分条件
C.充要条件 D.既不充分也非必要条件
15、对于函数，有下列五个命题：
（1）若存在反函数，且与反函数图像有公共点，则公共点肯定在直线上
（2）若在上有概念，则肯定是偶函数
（3）若是偶函数，且有解，则解的个数肯定是偶数
（4）若
是函数的周期，则
，也是函数的周期
（5）是函数为奇函数的充分非必要条件
从中任意抽取一个，恰好是真命题的概率为（ ）
A.1/5 B.2/5 C. 3/5 D.4/5
16、概念：假如一个向量从第二项起，每一项与他的前一项的差都等于同一个常向量，那样这个向量列叫做等差向量列，这个常向亮叫做等差向量列的公差
已知向量列是以为首相，公差
的等差向量列，若向量
与非零向量垂直，则
（ ）
A.
B.C. D.
解答卷
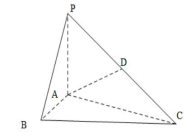
17、如图，在三棱锥
中，
底面，是的中点，已知，
求（1）三棱锥的体积
（2）异面直线与所成的角的大小（结果用三角函数值表示）
18、已知向量
，函数
（1）求函数的最小正周期及单调递增区间
（2）在
中，三内角的对边分别为，已知函数的图像经过点成等差数列，且
，求的值
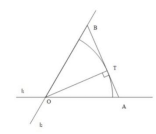
19、如图，在某商业区周围有两条公路
和，在点处交汇，该商业区为圆心角
半径
的扇形，现规划在该商业区外修建一条公路，与,分别交于，需要与扇形弧相切，切点T不在,上
（1）设，试用表示新建公路的长度，求出满足的关系式，并写出的范围
（2）设，试用表示新建公路的长度，并且确定的地方，使得新建公路的长度最短
20、已知函数（是非零实常数）满足且方程
有且仅有一个实数解。
（1）求的值
（2）当时，不等式恒成立，求实数的取值范围
（3）在直角坐标系中，求定点到函数图像上的任意一点的距离的最小值，并求获得最小值时的值
21、对于数列，若
（是与
无关的常数,）则称数列叫做“弱等差数列”已知数列满足：
且,对于
恒成立，（其中都是常数）
（1）求证：数列是“弱等差数列”，并求出数列的通项公式
（2）当
时，若数列是单调递增数列，求的取值范围
（3）若，且，数列满足：求
